Playing with words can be fun, if done in moderation.

So when we refer to Aikido (or any martial discipline) as an ideal discipline for the integral development of the individual, we are faced with three chances.

If we are equipped with a standard, well-operating brain, we read the sentence for what it is: Aikido (or any martial discipline) can be of use for the development of all the components of a person.

If we are particularly twisted, we write on a blog and we have sweated blood attending Engineering, we can think about the integral of Mathematical Analysis and try to make some reflection.

And it is this path that we take, without ending up discussing mathematics or making speeches that we wouldn’t understand either.

In Mathematics it is said that the integral of a function is another function plus an arbitrary constant.

This result is also called antiderivative. In fact, if we take this result and calculate the derivative, we return to the starting function, given that the derivative of a constant is always equal to zero.

Simple, right? Bah!

Let’s try to see integral and derivative not as two pillars of mathematics but as two tools to understand our trajectory.

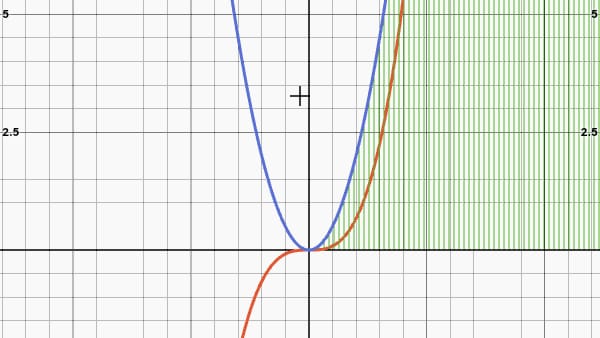
Simplifying a lot, we can say that the integral is (also) a way of measuring the area enclosed by a graph in a certain range. In other words, the ability to integrate is nothing more than the skill to consciously “fill” a trajectory.

However, mathematics tells us that every time we make the effort to integrate, an arbitrary variable of undefined value appears.

What? I invest time, money and sweat to try to change something about myself, to try to smooth out those parts of me that always seem the same and I discover that the result is obtaining a different myself also because it has… infinite constants!

Yes, because integration makes sense if verified with its complementary operation, derivation. That is, with a system capable of verifying the change, the evolution of a function, of a trajectory, in a given interval.

Mathematics teaches that, in fact, the derivative of a constant is always zero. If something is constant and does not change, growth cannot be appreciated.

But if the integration of our trajectory returns a result, together with some constants, then we can and must have the courage to measure our evolution.

Here are some simple thoughts.

Each of us has a trajectory: sometimes we define our existence as a parabola, which is a mathematical term.

Within this trajectory we can equip (or not) ourselves with awareness tools to fully experience our time interval.

Martial Arts, like any other work on oneself and like all integral development paths, modify us and sculpt our beliefs. Sometimes modifying them, sometimes strengthening what we already were, sometimes inserting new ones.

There is sometimes an underlying  idea in some practice environments where it is believed that having strong beliefs is exclusively a sign of mental rigidity and that, ultimately, practice should return a sort of limbo without them.

But life, even before mathematics, which is one of its languages, teaches exactly the opposite. Change and integration return constants, which are the anchors on which the measurement of the growth and evolution of our being is based. Getting to have fixed points is an achievement to strive for, not a threat to be dodged.

This, together with the difficulties linked to the physical aspect of the techniques, is the reason behind the crises that the practice cyclically goes through – together with the rest of our existence.

In fact, if we just measure the derivative in a very narrow range, we might see that instead of growing we are actually getting worse. And this too is not only real but also necessary: in order to grow and improve, our system must accept to struggle, to sometimes go into apnea, in order to set a stable evolution trajectory.

Obviously this is scary and conflicts with the habit and desire to obtain results immediately.

But the results can be seen from a distance. And if it is true that sometimes we define our life as a parabola, well, if we do the integral of a parabola we must admit that its area has a value that we cannot quantify…

Because integration is a neverending process.